手机直线：
咨询热线：0571-56211150
部分充填混凝土钢箱连续梁是一种在中间支座区段全截面和跨中区段钢箱截面受压区充填混凝土而形成的钢箱连续梁。其截面承载能力与连续梁的内力分布具有良好的适应性。文献对部分充填混凝土钢箱简支梁的抗弯、抗扭、抗剪、局部稳定等性能进行了试验和理论分析；文献对其在吊车梁改造中的应用进行了总结。
在简支梁研究的基础上，为研究充填混凝土对钢箱连续梁受力性能的影响，进行了2个两跨部分充填混凝土钢箱连续梁模型和一个空钢箱连续梁模型的加载试验；利用ANSYS分析软件，对试验梁进行了空间非线性有限元分析，基于有限元分析模型，对影响承载能力的主要参数进行了分析；进行了部分充填混凝土钢箱连续吊车梁的试设计，与简支吊车梁进行比较。
P1和P2为部分充填混凝土钢箱连续梁模型，两者仅钢箱顶板和腹板厚度不同，前者为3mm，后者为2mm。模型P1和H1钢箱尺寸相同，模型H1为空钢箱连续梁。通过分配梁将两个集中荷载对称于中间支座施加在试验梁上，分配梁计算跨径2.9m。
钢板为Q235钢材，标准试验实测屈服强度为293N/m2，抗拉强度为400 N/m2。混凝土设计强度等级为C40，试验时实测立方体抗压强度为43 N/m2。
试验梁模型的荷载-挠度曲线，模型P1和P2的极限荷载分别为540kN和440kN，荷载在极限荷载的70%以下时，挠度与荷载近于线性关系；荷载达到极限荷载的70%~95%之间，挠度与荷载呈弹塑性关系；荷载达到极限荷载的95%后模型进入塑性破坏阶段，挠度急剧增加，破坏过程表现为塑性破坏。
模型H1承受的最大荷载为280kN，在破坏前基本处于线弹性工作阶段，中间支座处钢箱腹板局部屈曲，引起截面承载能力突然下降而破坏，表现为脆性破坏。
模型P1与H1钢箱截面尺寸相同，试验结果表明，部分充填混凝土后的模型P1比空钢箱模型H1承受的最大荷载增大了1.9倍。
由P1截面弯矩-曲率关系可见，P1跨中截面弯矩达到极限弯矩的67%前，弯矩与曲率呈线性关系，在荷载达到极限荷载的67%后，跨中钢箱底板开始屈服，跨中截面曲率迅速发展，荷载在极限荷载的90%后，截面大部分进入塑性状态；当中支座截面弯矩达到极限弯矩的72%前，弯矩与曲率呈线性关系，在荷载达到极限荷载的80%后，截面曲率迅速发展，截面大部分很快进入塑性状态。
从P2截面弯矩-曲率关系可以看出，P2跨中截面弯矩达到极限弯矩的70%前，弯矩与曲率呈线性关系，在荷载达到极限荷载的70%后，跨中钢箱底板开始屈服，跨中截面曲率迅速发展，荷载在极限荷载的95%后，截面大部分进入塑性状态；当中支座截面弯矩达到极限弯矩的85%前，弯矩与曲率呈线性关系，在荷载达到极限荷载的85%后，截面曲率迅速发展，截面大部分很快进入塑性状态。
从H1截面弯矩-曲率关系可以看出，H1试验受载过程中弯矩与曲率基本呈线性关系，破坏前跨中截面钢箱顶板开始屈服，中支座截面钢箱顶板进入屈服阶段。
实验结果表明，部分充填混凝土钢箱连续梁试验模型P1和P2跨中截面延性(ψus/ψys)为8.3~8.5，中支座截面延性(ψus/ψys) 为10.0~15.5；P1跨中截面Mus提高100%，中支座截面提高84%，P1中支座截面延性是H1 的9.7倍，P1跨中截面延性是H1的8.3倍。
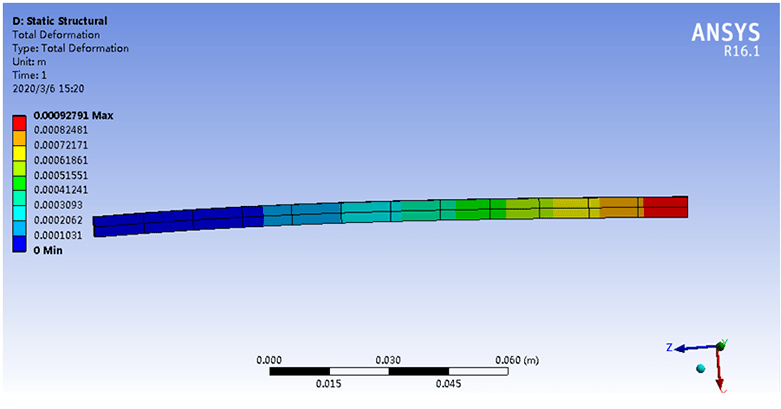
计算机软硬件技术的发展，可以利用有限元法更真实地模拟组合梁的受力过程。本项目采用ANSYS软件对部分充填混凝土钢箱连续试验梁进行了空间有限元非线性分析。
专业从事有限元分析公司│有限元分析│CAE分析│FEA分析│技术服务与解决方案
杭州那泰科技有限公司
本文出自杭州那泰科技有限公司www.vwnkzix.cn，转载请注明出处和相关链接！